Graph Search
Published:
While diving into autograd internals, I had this ambitious goal to crack the mystery of Topological sort — an important step in backpropagation. But just studying it alone felt like buying a single sock. Since I needed to brush up on Depth-First Search anyway (Topological sort’s older sibling), I figured, why not toss Breadth-First Search into the cart too? After all, who goes shopping for algorithms and leaves with just one?
import random
import matplotlib.pyplot as plt
import numpy as np
from IPython import display
Toy Problem
We will pick a problem of finding a path from the origin (top-left) to the sink (bottom-right) of a randomly generated maze. A maze is a mesh of cells with distinct paths that can (or cannot) be traversed, it is a graph. There are several ways to encode a graph. Here, we will encode graph as an adjacency matrix, with 1 representing a wall and 0 representing a pathway.
def draw(maze: np.ndarray):
"""Auto-updating plot (note: only if in running in a notebook)"""
display.clear_output(wait=True)
plt.figure(figsize=(4, 4))
plt.axis("off")
plt.imshow(maze, cmap="plasma_r")
plt.show()
I will use a simple recusive backtracking algorithm to generate mazes. Here is a goldmine of other algorithms (with beautiful animations) if you are interested.
def generate_maze(n: int) -> np.ndarray:
"""Generates a random N*N maze using recursive backtracking."""
# Make `n` odd. Why?
n -= (n % 2)
n += 1
maze = np.ones((n, n), dtype=np.int32)
# Opening at the top and bottom. We choose these points
# because we can guarantee that an odd-maze will not have doubly-thick walls.
maze[0][1] = maze[-1][-2] = 0
# Direction vectors. Moving by 2 units ensures
# that we skip over the walls and move from one potential passage to next.
directions = [(0, 2), (0, -2), (2, 0), (-2, 0)]
# Choose a random odd coordinate.
start = (random.randrange(1, n, 2), random.randrange(1, n, 2))
maze[start] = 0
stack = [start]
while stack:
cy, cx = stack[-1]
# Get neighbors in a random order.
random.shuffle(directions)
found_unvisited_neighbor = False
for dx, dy in directions:
nx, ny = cx + dx, cy + dy
# Check if the candidate cell is not out of bounds and is a wall.
if (0 <= nx < n and 0 <= ny < n and maze[ny][nx] == 1):
# Pave thru the wall.
maze[ny][nx] = 0
maze[cy + dy // 2][cx + dx // 2] = 0
# Append new location for paving
stack.append((ny, nx))
found_unvisited_neighbor = True
break
# Backtrack if all neighbors have been visited.
if not found_unvisited_neighbor:
stack.pop()
return maze
random.seed(42)
maze = generate_maze(50)
draw(maze)
def get_neighbors(y, x):
return [
(y + dy, x + dx)
for dy, dx in [(1, 0), (-1, 0), (0, 1), (0, -1)]
]
Our goal is to search for a path from the origin (top-left) to sink (bottom-right). During our maze traversal, we will explore neighbors one step away.
Depth-First Search
A key feature of this search is that it exhaustively searches through all possible sub-vertices connected to a given vertex, before backtracking and moving to a different vertex at the same level. It is oblivious to how close it might be to its goal. Other words, even if it is very close to a solution, and then yeets off to a random sub-vertex, it will not return until it has exhaustively searched that dead end.
Tip: Run this in a notebook for an auto-updating plot.
def dfs(graph: np.ndarray,
start: tuple[int, int] = (0, 1),
end: tuple[int, int] = (-1, -2),
visualize: bool = False) -> bool:
"""Checks if a path exists between `start` and `end`."""
visited = np.zeros_like(graph).astype(np.bool_)
candidates = [start]
visited[start] = True
found = False
while candidates:
if visualize: draw(np.where(visited, 0.5, maze))
# Pick the most recent candidate, i.e. LIFO
cy, cx = candidates.pop(-1)
if visited[end]:
found = True
break
for ny, nx in get_neighbors(cy, cx):
if (
# within bounds?
0 <= ny < graph.shape[0] and
0 <= nx < graph.shape[1] and
not visited[ny][nx] and
# not a wall?
graph[ny][nx] != 1
):
candidates.append((ny, nx))
visited[ny][nx] = True
return found
dfs(maze, visualize=True)
DFS search time is proportional to the number of vertices in our adjacency matrix - \(O(N^2)\). The space required to store intermediate states is proportional to the number of vertices (since visited array and candidates stack are the only auxiliary objects in our function), therefore \(O(N^2)\).
Breadth-First Search
A natural modification to DFS could be made on candidate selection. In fact, all the search algorithms we will see today are merely intelligent ways of ‘choosing where to search’.
Instead of going down the rabbit-hole on a single vertex, what if we first explore all vertices available at a given level?
Tip: Run this in a notebook for an auto-updating plot.
def bfs(graph: np.ndarray,
start: tuple[int, int] = (0, 1),
end: tuple[int, int] = (-1, -2),
visualize: bool = False) -> bool:
"""Checks if a path exists between `start` and `end`."""
visited = np.zeros_like(graph).astype(np.bool_)
candidates = [start]
visited[start] = True
found = False
while candidates:
if visualize: draw(np.where(visited, 0.5, maze))
# Pick candidates in the order they were added, i.e. FIFO.
# Observe that this is the *only* change from DFS!
cy, cx = candidates.pop(0)
if visited[end]:
found = True
break
for ny, nx in get_neighbors(cy, cx):
if (
# within bounds?
0 <= ny < graph.shape[0] and
0 <= nx < graph.shape[1] and
not visited[ny][nx] and
# not a wall?
graph[ny][nx] != 1
):
candidates.append((ny, nx))
visited[ny][nx] = True
return found
bfs(maze, visualize=True)
BFS has the same time and space complexity as DFS in this example - \(O(N^2)\). It also feels parallel. It is because it switches between candidates very quickly - exploring horizontally across each level before exhausting and going to the next level in depth.
Note: We can do a microbenchmark to see that neither of DFS or BFS is relatively faster. This is an expected outcome for large, uniformly random mazes. Real world graphs typically carry structure bias towards depth (or width). Hence, choice of DFS/BFS should be informed by the structure of the graph.
# takes ~1 min
%timeit -n 5 -r 10 dfs(generate_maze(500))
%timeit -n 5 -r 10 bfs(generate_maze(500))
749 ms ± 58.2 ms per loop (mean ± std. dev. of 10 runs, 5 loops each)
778 ms ± 58.8 ms per loop (mean ± std. dev. of 10 runs, 5 loops each)
Topological Sort
Now to the intended goalpost - topological sort. It helps to understand why we need it in the first place. Neural networks are directed acyclic graphs that take a set of input tensor(s), and through multiple parameterized transformations, return a set of output tensor(s).
We will emulate a different toy problem; by generating sparsely-connected perceptrons. We control sparsity using a parameter. Note that if sparsity is too high (say above 0.5), you may end up with graphs unconnected with inputs or outputs. It won’t impact our computation though. You can experiment with different values to understand how toposort identifies viable orderings.
Bear with me on this boilerplate code to visualize our graph, before we implement toposort(...).
import itertools
import networkx as nx
def generate_mlp(
layers: list[int],
sparsity: float = 0.,
seed: int = 42
) -> tuple[nx.DiGraph, dict]:
"""Generate a layer-wise sparsely connected MLP.
Args:
layers: A list of integers denoting nodes in each layer. First and
last are considered input and output nodes respectively.
sparsity: A float between [0, 1] representing how sparse the graph
should be. 0 means no sparsity, i.e. a fully-connected MLP.
seed: For reproducibility.
Returns:
A tuple of nx.DiGraph and options to plot it pretty.
"""
random.seed(seed)
num_layers = len(layers)
# Assign labels to each node.
input_nodes = [f"$x_{i}$" for i in range(layers[0])]
hidden_layers = [
[f"$h^{lyr}_{i}$" for i in range(layers[lyr])]
for lyr in range(1, num_layers - 1)
]
output_nodes = [f"y{i}" for i in range(layers[-1])]
layers = [input_nodes, *hidden_layers, output_nodes]
# Assign nodes.
G = nx.DiGraph()
for lyr, nodes in enumerate(layers):
G.add_nodes_from(nodes, layer=lyr)
# Assign random edges.
for left_layer, right_layer in zip(layers[:-1], layers[1:]):
connections = list(itertools.product(left_layer, right_layer))
keep_p = 1 - sparsity
G.add_edges_from(connections[:int(keep_p * len(connections))])
# Pretty plot.
pos = nx.multipartite_layout(G, subset_key="layer")
colors = ["gold"] + ["violet"] * (num_layers - 2) + ["limegreen"]
options = {
"node_color": [colors[data["layer"]] for node, data in G.nodes(data=True)],
"with_labels": True,
"node_size": 1000,
"pos": pos,
}
return G, options
G, options = generate_mlp([3, 4, 6, 4, 6, 1], sparsity=0.5)
nx.draw(G, **options)
plt.show()
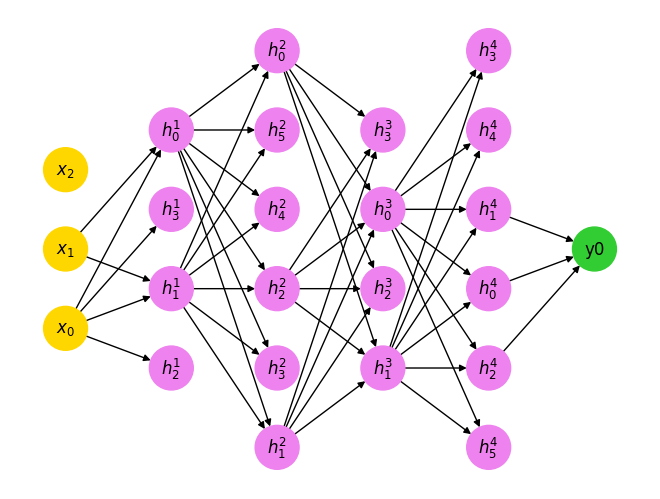
You can play around with various layer sizes and sparsities. The only important observation is that not all ancestor nodes may influence the output loss node (indexed as \(y_i\)).
The training objective of neural networks is often to minimize this loss by moving along the derivative and backpropagating gradients from the terminal node to the inputs. Each node in a neural network ‘knows’ how to compute its own derivative only if a gradient signal from the nodes succeeding it is available.
But in a graph with (easily) hundreds of nodes and edges, the autograd engine must know the exact order of reverse traversal.
In other words, for a root node loss, the autograd engine needs a list of all dependencies to loss all the way to input tensor(s), in the order they impact it. This is like searching along the depth from the loss node: depth-first search! We will use toposort to find these orderings from a given root node to the stopping points on the graph (i.e. nodes with no more ancestors).
def toposort(G: nx.DiGraph, root: str):
"""Returns a topological ordering from `root` on the graph `G`."""
visited = set()
order = []
def _dfs(node):
if node not in visited:
visited.add(node)
# If the node has ancestors, DFS along each.
for parent in G.predecessors(node):
_dfs(parent)
# Once all ancestors have been evaluated,
# add the node to the topological order.
order.append(node)
# Start searching for stopping points from the root.
_dfs(root)
# Because we start from the root node.
order.reverse()
return order
order = toposort(G, 'y0')
order
['y0',
'$h^4_2$',
'$h^4_1$',
'$h^4_0$',
'$h^3_1$',
'$h^3_0$',
'$h^2_2$',
'$h^2_1$',
'$h^2_0$',
'$h^1_1$',
'$h^1_0$',
'$x_1$',
'$x_0$']
Modulo the ugly \(\LaTeX\) formatting, We can see that toposort returns an ordering from output node(s) to input node(s) whenever there is a path connecting them.
Let’s draw these backward edges.
def draw_backward_traversal(G: nx.DiGraph, order: list[str]):
"""Plots the reverse traversal of nodes given in `order` on the graph `G`."""
edges = []
for node in order:
# Point incident edges backwards
incident_edges = G.in_edges(node)
incident_edges = [e[::-1] for e in incident_edges]
edges.extend(incident_edges)
nx.draw(G, edgelist=edges, edge_color="red", **options)
plt.show()
draw_backward_traversal(G, order)
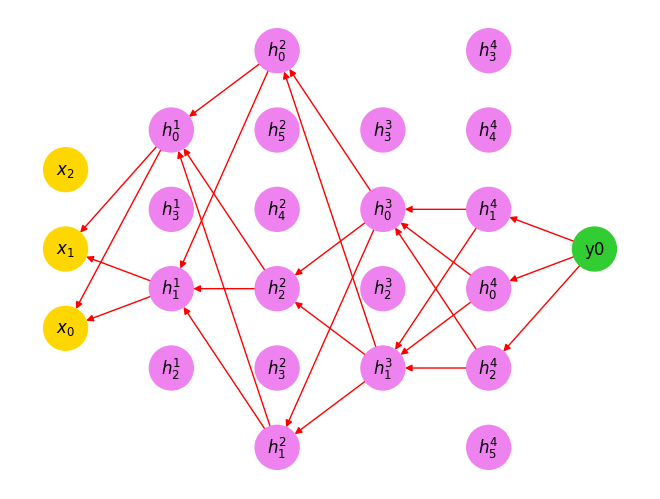
See? The topological ordering automatically ignores nodes (even inputs) that do not influence the output.
N.B: This is a possibly unconventional example of sparsely-connected MLPs. In practice, MLPs are trained fully-connected. I should have used a better terminology, in that these graph nodes are arbitrary functions themselves. But I am sure it gets the idea across.
We knew it all along, didn’t we?
This exercise taught me that algorithms of this class are actually straightforward to understand if you have a view of the entire graph and you know the objective. The challenge lies in expressing your computation in a way computers can understand. Specifically:
- How can you identify a sub-problem that can be recursed/iterated over.
- How and when to recurse/iterate over that subproblem, and
- How to book-keep states efficiently.
We take for granted how much our brain does this in a diffused manner. Luckily, with frontier language models getting better, ‘talking’ with computers will get easier.
I hoped to cover Dijkstra and A* as well, given how they add a sprinkle of intelligence (read heuristics) to solve certain classes of graph problems faster. That will be a different article for now.